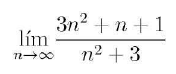Aula Virtual, Exámenes Resueltos, PAU UNED, Pruebas de Acceso a la Universidad
Examen UNED PCE resuelto Matemáticas II Ciencias Mayo-Junio 2019
CARACTERÍSTICAS DE LA PRUEBA
La prueba de evaluación consistirá en diez preguntas de tipo test y dos problemas cuyas soluciones tendrá que desarrollar y escribir el estudiante durante la prueba.
1. Parte de preguntas de tipo test: Constará de diez preguntas, cada una con tres posibles alternativas. El estudiante deberá elegir la alternativa que considere correcta; una y una sola de las alternativas es correcta.
– Cada pregunta correcta sumará 0’5 puntos
– Cada pregunta incorrecta restará 0’15 puntos – Las preguntas en blanco no suman ni restan puntos
– Si la aplicación de los criterios anteriores condujera a una puntación negativa se asignará una puntuación igual a cero, por lo que puntación de esta parte estará comprendida entre 0 y 5 puntos.
2. Parte de problemas: Constará de dos problemas característicos de la asignatura, cuyo planteamiento, desarrollo y resolución requiera los conocimientos matemáticos de los bloques de contenidos.
Constará de 2 preguntas, no siendo obligatorio contestar a todas las cuestiones. La calificación máxima de este bloque es de 5 puntos.
PREGUNTAS Y TIPOLOGÍA CONTENIDOS DEL TEMARIO
Preguntas abiertas Bloques 1,2,3,4 y 5
Preguntas de opción múltiple Bloques: 2,3,4 y 5
INSTRUCCIONES PARA EL DESARROLLO DE LA PRUEBA
– La duración total de la prueba será de 90 minutos.
– Se permitirá el uso de calculadoras no programables y sin capacidad gráfica.
– No se permitirán ordenadores personales, tabletas, teléfonos móviles o aparatos con capacidad de comunicación.
– La parte de preguntas abiertas se responderá en hojas diferentes a la de la parte objetiva.
Ambas partes se cumplimentarán con bolígrafo y se entregarán ambas partes simultáneamente.

1.- Si u = (0,3,5) y v = (1,-2,2) entonces el producto vectorial de ambos es:
a) uxv = (1,5,-3)
b) uxv = (11,5,-3)
c) uxv = (1,5,3)
La respuesta correcta es b)
2.- El punto P’ simétrico del punto P(1,0,1) respecto de la recta r(x,y,z)=(1,0,0) + λ(0,1,1)
a) P’ (1,1,1)
b) P’ (1,1,0)
c) P’ (-1,1,-1)
La respuesta correcta es b)
3.- La distancia del punto P(4,6,0) al plano es: π: 2x-y+2z+1=0
a) 1
b) 2
c) 3
La respuesta correcta es a)
4.- Dado el plano π y la recta r de ecuaciones: π: x+2y-z=2 se verifica que:
a) La recta es paralela al plano y no se cortan
b) Se cortan en un punto
c) La recta está contenida en el plano
La respuesta correcta es c)
5.- La ecuación del plano que es ortogonal a la recta y pasa por el punto P(1,1,1) es: r: x=y-1=z
a) x+y+z=3
b) x-y+z=1
c) x+y+z=1
La respuesta correcta es a)
6.- El valor del siguiente límite es:
a) 3
b) No existe
c) Infinito
La respuesta correcta es a)
7.- Sea la matriz 3×3 tal que: A3 =-1
a) A10 = A
b) A10 = -A
c) A10 = 1
La respuesta correcta es b)
8.- Dados dos sucesos de un experimento aleatorio A y B, con probabilidades: P(A) = 4/9 P(B) =1/3 P(AUB) = 2/3
a) p(AlB) = 4/9
b) p(AlB) = 2/9
c) p(AlB) = 1/3
La respuesta correcta c)
9.- En un bolsa hay 10 bolas rojas, 15 amarillas y 5 azules. Si se extraen dos bolas sin reemplazamiento la probabilidad de que las dos sean rojas es:
a) 3/29
b) 1/3
c) 9/29
La respuesta correcta es a)
10.- En una clase de 12 estudiantes se quieren hacer grupos de tres estudiantes para realizar un trabajo. ¿ Cuántos grupos distintos se pueden hacer?.
a) 13220
b) 660
c) 220
La respuesta correcta es c)
Os dejamos los siguientes vídeos del examen resueltos y explicados de Matemáticas II Ciencias PCE UNED
Esperamos que os sea de mucha ayuda!